SQL, langage algébrique

Le second langage étudié dans ce cours est l’algèbre relationnelle. Elle consiste en un ensemble d’opérations qui permettent de manipuler des relations, considérées comme des ensembles de nuplets : on peut ainsi faire l’union ou la différence de deux relations, sélectionner une partie des nuplets la relation, effectuer des produits cartésiens ou des projections, etc.

Important

nous voyons maintenant les relations comme des ensembles, au sens mathématique du terme, avec au moins deux conséquences importantes:

  • il n’y pas de doublon dans un ensemble, donc tous les opérateurs éliminent implicitement tout potentiel doublon dansn le résultat ;

  • un ensemble n’est pas ordonné: en aucun cas on ne peut donc s’appuyer sur l’hypothèse d’un ordre sur les nuplets.

On peut voir l’algèbre relationnelle comme un langage de programmation très simple qui permet d’exprimer des requêtes sur une base de données relationnelle. C’est donc plus une approche d’informaticien que de logicien. Elle correspond moins naturellement à la manière dont on pense une requête. À l’origine, le langage SQL était d’ailleurs entièrement construit sur la logique mathématique, comme nous l’avons vu dans le chapitre SQL, langage déclaratif, à l’exception de l’union et de l’intersection. L’algèbre n’était utilisée que comme un moyen de décrire les opérations à effectuer pour évaluer une requête. Petit à petit, les évolutions de la norme SQL ont introduit dans le langage les opérateurs de l’algèbre. Il est maintenant possible de les retrouver tous et d’exprimer toutes les requêtes (plus ou moins facilement) avec cette approche. C’est ce que nous étudions dans ce chapitre.

Note

La base utilisée comme exemple dans ce chapitre est celle de nos intrépides voyageurs, présentée dans le chapitre Le modèle relationnel.

S1: Les opérateurs de l’algèbre

Supports complémentaires:

L’algèbre se compose d’un ensemble d’opérateurs, parmi lesquels 6 sont nécessaires et suffisants et permettent de définir les autres par composition. Une propriété fondamentale de chaque opérateur est qu’il prend une ou deux relations en entrée, et produit une relation en sortie. Cette propriété (dite de clôture) permet de composer des opérateurs : on peut appliquer une sélection au résultat d’un produit cartésien, puis une projection au résultat de la sélection, et ainsi de suite. En fait on peut construire des expressions algébriques arbitrairement complexes qui permettent d’effectuer toutes les requêtes relationnelles à l’aide d’un petit nombre d’opérations de base.

Ces opérations sont donc:

  • La sélection, dénotée \(\sigma\)

  • La projection, dénotée \(\pi\)

  • Le renommage, dénoté \(\rho\)

  • Le produit cartésien, dénoté \(\times\)

  • L’union, \(\cup\)

  • La différence, \(-\)

Les trois premiers sont des opérateurs unaires (ils prennent en entrée une seule relation) et les autres sont des opérateurs binaires. À partir de ces opérateurs il est possible d’en définir d’autres, et notamment la jointure, \(\Join\), qui est la composition d’un produit cartésien et d’une sélection. C’est une opération essentielle, nous lui consacrons la prochaine session.

Ces opérateurs sont maintenant présentés tour à tour.

La projection, \(\pi\)

La projection \(\pi_{A_1, A_2, \ldots,A_k}(R)\) s’applique à une relation \(R\), et construit une relation contenant tous les nuplets de \(R\), dans lesquels seuls les attributs \(A_1, A_2, \ldots A_k\) sont conservés. La requête suivante construit une relation avec le nom des logements et leur lieu.

\[\pi_{nom, lieu}(Logement)\]

On obtient le résultat suivant, après suppression des colonnes id, capacité et type :

nom

lieu

Causses

Cévennes

Génépi

Alpes

U Pinzutu

Corse

Tabriz

Bretagne

En SQL, le projection s’exprime avec le select suivi de la liste des attributs à projeter.

select nom, lieu
from Logement

C’est un habillage syntaxique direct de la projection.

Si on souhaite conserver tous les attributs, on peut éviter d’en énumérer la liste en la remplaçant par *.

select *
from Logement

Note

En algèbre cette requête est tout simplement l’identité: \(R\)

La sélection, \(\sigma\)

La sélection \(\sigma_F(R)\) s’applique à une relation, \(R\), et extrait de cette relation les nuplets qui satisfont un critère de sélection, \(F\). Ce critère peut être :

  • La comparaison entre un attribut de la relation, \(A\), et une constante \(a\). Cette comparaison s’écrit \(A \Theta a\), où \(\Theta\) appartient à \(\{=, <, >, \leq, \geq\}\).

  • La comparaison entre deux attributs \(A_1\) et \(A_2\), qui s’écrit \(A_1 \Theta A_2\) avec les mêmes opérateurs de comparaison que précédemment.

Premier exemple : exprimer la requête qui donne tous les logements en Corse.

\[\sigma_{lieu='Corse'}(Logement)\]

On obtient donc le résultat :

code

nom

capacité

type

lieu

pi

U Pinzutu

10

Gîte

Corse

La sélection a pour effet de supprimer des nuplets, mais chaque nuplet garde l’ensemble de ses attributs. Il ne peut pas y avoir de problème de doublon (pourquoi?) et il ne faut donc surtout par appliquer un distinct.

En SQL, les critères de sélection sont exprimés par la clause where.

select *
from Logement
where lieu = 'Corse'

Les chaînes de caractères doivent impérativement être encadrées par des apostrophes simples, sinon le système ne verrait pas la différence avec un nom d’attribut. Ce n’est pas le cas pour les numériques, car aucun nom d’attribut ne peut commencer par un chiffre.

select *
from Logement
where capacité = 134

Note

Vous noterez que SQL appelle select la projection, et where la sélection, ce qui est pour le moins infortuné. Dans des langages modernes comme XQuery (pour les modèles basés sur XML) le, select est remplacé par return. En ce qui concerne SQL, la question a donné lieu (il y a longtemps) à des débats mais il était déjà trop tard pour changer.

Le produit cartésien, \(\times\)

Le premier opérateur binaire, et le plus utilisé, est le produit cartésien, \(\times\). Le produit cartésien entre deux relations \(R\) et \(S\) se note \(R \times S\), et permet de créer une nouvelle relation où chaque nuplet de \(R\) est associé à chaque nuplet de \(S\).

Voici deux relations, la première, \(R\), contient

A

B

a

b

x

y

et la seconde, \(S\), contient :

C

D

c

d

u

v

x

y

Et voici le résultat de \(R \times S\) :

A

B

C

D

a

b

c

d

a

b

u

v

a

b

x

y

x

y

c

d

x

y

u

v

x

y

x

y

Le nombre de nuplets dans le résultat est exactement \(|R| \times |S|\) (\(|R|\) dénote le nombre de nuplets dans la relation \(R\)).

En lui-même, le produit cartésien ne présente pas un grand intérêt puisqu’il associe aveuglément chaque nuplet de \(R\) à chaque nuplet de \(S\). Il ne prend vraiment son sens qu’associé à l’opération de sélection, ce qui permet d’exprimer des jointures, opération fondamentale qui sera détaillée plus loin.

En SQL, le produit cartésien est un opérateur cross join intégré à la clause from.

select *
from R cross join S

C’est la première fois que nous rencontrons une expression à l’intérieur du from en lieu et place de la simple énumération par une virgule. Il y a une logique certaine à ce choix: dans la mesure où R cross join S définit une nouvelle relation, la requête SQL peut être vue comme une requête sur cette seule relation, et nous sommes ramenés au cas le plus simple.

Comme illustration de ce principe, voici le résultat du produit cartésien \(Logement \times Activité\) (en supprimant l’attribut description pour gagner de la place).

code

nom

capacité

type

lieu

codeLogement

codeActivité

ca

Causses

45

Auberge

Cévennes

ca

Randonnée

ge

Génépi

134

Hôtel

Alpes

ca

Randonnée

pi

U Pinzutu

10

Gîte

Corse

ca

Randonnée

ta

Tabriz

34

Hôtel

Bretagne

ca

Randonnée

ca

Causses

45

Auberge

Cévennes

ge

Piscine

ge

Génépi

134

Hôtel

Alpes

ge

Piscine

pi

U Pinzutu

10

Gîte

Corse

ge

Piscine

ta

Tabriz

34

Hôtel

Bretagne

ge

Piscine

ca

Causses

45

Auberge

Cévennes

ge

Ski

ge

Génépi

134

Hôtel

Alpes

ge

Ski

pi

U Pinzutu

10

Gîte

Corse

ge

Ski

ta

Tabriz

34

Hôtel

Bretagne

ge

Ski

ca

Causses

45

Auberge

Cévennes

pi

Plongée

ge

Génépi

134

Hôtel

Alpes

pi

Plongée

pi

U Pinzutu

10

Gîte

Corse

pi

Plongée

ta

Tabriz

34

Hôtel

Bretagne

pi

Plongée

ca

Causses

45

Auberge

Cévennes

pi

Voile

ge

Génépi

134

Hôtel

Alpes

pi

Voile

pi

U Pinzutu

10

Gîte

Corse

pi

Voile

ta

Tabriz

34

Hôtel

Bretagne

pi

Voile

C’est une relation (tout est relation en relationnel) et on peut bien imaginer interroger cette relation comme n’importe quelle autre. C’est exactement ce que fait la requête SQL suivante.

select *
from Logement cross join Activité

Jusqu’à présent, le from ne contenait que des relations « basées » (c’es-à-dire stockées dans la base). Maintenant, on a placé une relation calculée. Le principe reste le même. Rappelons que l’algèbre est un langage clos: il s’applique à des relations et produit une relation en sortie. Il est donc possible d’appliquer à nouveau des opérateurs à cette relation-résultat. C’est ainsi que l’on construit des expressions, comme nous allons le voir dans la session suivante. Nous retrouverons une autre application de cette propriété extrêmement utile quand nous étudierons les vues (chapitre Schémas relationnel).

Renommage

Quand les schémas des relations \(R\) et \(S\) sont complètement distincts, il n’y a pas d’ambiguité sur la provenance des colonnes dans le résultat. Par exemple on sait que les valeurs de la colonne \(A\) dans \(R \times S\) viennent de la relation \(R\). Il peut arriver (il arrive de fait très souvent) que les deux relations aient des attributs qui ont le même nom. On doit alors se donner les moyens de distinguer l’origine des colonnes dans la relation résultat en donnant un nom distinct à chaque attribut.

Voici par exemple une relation \(T\) qui a les mêmes noms d’attributs que \(R\).

A

B

m

n

o

p

Le schéma du résultat du produit cartésien \(R \times T\) a pour schéma \((A, B, A, B)\) et présente donc des ambiguités, avec les colonnes \(A\) et B en double.

La première solution pour lever l’ambiguité est d’adopter une convention par laquelle chaque attribut est préfixé par le nom de la relation d’où il provient. Le résultat de \(R \times T\) devient alors :

R.A

R.B

T.A

T.B

a

b

m

n

a

b

o

p

x

y

m

n

x

y

o

p

Cette convention pose quelques problèmes quand on crée des expressions complexes. Il existe une seconde possibilité, plus générale, pour résoudre les conflits de noms : le renommage. Il s’agit d’un opérateur particulier, dénoté \(\rho\), qui permet de renommer un ou plusieurs attributs d’une relation. L’expression \(\rho_{A \to C,B \to D}(T)\) permet ainsi de renommer \(A\) en \(C\) et \(B\) en \(D\) dans la relation \(T\). Le produit cartésien

\[R \times \rho_{A\to C,B \to D}(T)\]

ne présente alors plus d’ambiguités. Le renommage est une solution très générale, mais asez lourde à utiliser

Il est tout à fait possible de faire le produit cartésien d’une relation avec elle-même. Dans ce cas le renommage où l’utilisation d’un préfixe distinctif est impératif. Voici par exemple le résultat de \(R \times R\), dans lequel on préfixe par \(R1\) et \(R2\) respectivement les attributs venant de chacune des opérandes.

R1.A

R1.B

R1.A

R2.B

a

b

a

b

a

b

x

y

x

y

a

b

x

y

x

y

En SQL, le renommage est obtenu avec le mot-clé as. Il peut s’appliquer soit à la relation, soit aux attributs (ou bien même aux deux). Le résultat suivant est donc obtenu avec la requête:

select *
from R as R1 cross join R as R2

On obtient une relation de schéma (R1.A, R1.B, R1.A, R2.B), avec des noms d’attribut qui ne sont en principe pas acceptés par la norme SQL. Il reste à spécifier ces noms en ajoutant dans as dans la clause de projection.

select R1.a as premier_a, R1.b as premier_b, R2.a as second_a, R2.b as second_b
from R as R1 cross R as R2

Ce qui donnera donc le résultat:

premier_a

premier_b

second_a

second_b

a

b

a

b

a

b

x

y

x

y

a

b

x

y

x

y

Sur notre schéma, le renommage s’impose par exemple si on effectue le produit cartésien entre Voyageur et Séjour car l’attribut idVoyageur apparaît dans les deux tables. Essayez la requête:

select Voyageur.idVoyageur, Séjour.idVoyageur
from Voyageur cross join Séjour

Elle vous renverra une erreur comme Encountered duplicate field name: “idVoyageur”. Il faut nommer explicitement les attributs pour lever l’ambiguité.

select Voyageur.idVoyageur as idV1, Séjour.idVoyageur as idV2
from Voyageur cross join Séjour

L’union, \(\cup\)

Il existe deux autres opérateurs binaires, qui sont à la fois plus simples et moins fréquemment utilisés.

Le premier est l’union. L’expression \(R \cup S\) crée une relation comprenant tous les nuplets existant dans l’une ou l’autre des relations \(R\) et \(S\). Il existe une condition impérative : les deux relations doivent avoir le même schéma, c’est-à-dire même nombre d’attributs, mêmes noms et mêmes types.

L’union des relations \(R(A,B)\) et \(S(C,D)\) données en exemple ci-dessus est donc interdite (on ne saurait pas comment nommer les attributs dans le résultat). En revanche, en posant \(S' = \rho_{C\to A,D\to B}(S)\), il devient possible de calculer \(R \cup S'\), avec le résultat suivant :

A

B

a

b

x

y

c

d

u

v

Comme pour la projection, il faut penser à éviter les doublons. Donc le nuplet (x,y) qui existe à la fois dans \(R\) et dans \(S'\) ne figure qu’une seule fois dans le résultat.

L’union est un des opérateurs qui existe dans SQL depuis l’origine. La requête suivante effectue l’union des lieux de la table Logement et des régions de la table Voyageur. Pour unifier les schémas, on a projeté sur cet unique attribut, et on a effectué un renommage.

select lieu from Logement
  union
select région as lieu from Voyageur

On obtient le résultat suivant.

lieu

Cévennes

Alpes

Corse

Bretagne

Auvergne

Tibet

Notez que certains noms comme « Corse » apparaîssent deux fois: vous savez maintenant comment éliminer les doublons avec SQL.

La différence, \(-\)

Comme l’union, la différence s’applique à deux relations qui ont le même schéma. L’expression \(R -S\) a alors pour résultat tous les nuplets de \(R\) qui ne sont pas dans \(S\).

Voici la différence de \(R\) et \(S'\), les deux relations étant définies comme précédemment.

A

B

a

b

En SQL, la différence est obtenue avec except.

select A, B from R
   except
select C as A, D as B from S

La différence est le seul opérateur algébrique qui permet d’exprimer des requêtes comportant une négation (on veut « rejeter » quelque chose, on « ne veut pas » des nuplets ayant telle propriété). La contrainte d’identité des schémas rend cet opérateur très peu pratique à utiliser, et on lui préfère le plus souvent la construction logique du SQL « déclaratif », not exists.

Note

L’opérateur except n’est même pas proposé par certains systèmes comme MYSQL.

Quiz

Que signifie la propriété dite « de clôture » pour l’algèbre relationnelle

  1. Que les opérateurs permettent de calculer par transitivité tous les nuplets accessibles à partir d’un nuplet particulier?

  2. Que l’entrée et la sortie des opérateurs appartient à un même ensemble, celui des relations, et que les calculs restent donc dans une monde « clos »?

  3. Qu’aucun opérateur ne peut se définir en fonction des autres

Pourquoi ne peut-il pas y avoir de doublon dans le résultat d’une sélection (appliquée à une relation en première forme normale)

  1. Parce que la formule de sélection définit une clé pour la relation résultat

  2. Parce que la sélection élimine les doublons

  3. S’il n’y a pas de doublon en entrée (1FN), à plus forte raison il n’y en a pas en sortie puisque la sélection ne fait qu’éliminer des nuplets

Quelle est la condition pour appliquer un produit cartésien?

  1. Les relations doivent avoir le même schéma

  2. Les relations doivent avoir des schémas distincts, sans nom d’attribut commun

  3. Les relations ont le même nombre de nuplets

Quelle est la condition pour appliquer une différence

  1. Les relations doivent avoir le même schéma

  2. Les relations doivent avoir des schémas distincts, sans nom d’attribut commun

  3. Les relations ont le même nombre de nuplets

Prenons deux relations \(R\) et \(S\), de même schéma. Quelle est l’expression qui calcule leur intersection?

  1. \(R - (R - S)\)

  2. \(((R \cup S) - S) - R)\)

  3. \(((R \times S) - S) - R)\)

Supposons que \(R\) a 12 nuplets et \(S\) 4. Les deux relations ont des schémas distincts. Quelle phrase est correcte ?

  1. \(R \times S\) a 16 nuplets

  2. \(R \times S\) a 12 nuplets

  3. \(R \times S\) a 48 nuplets

  4. \(R \times S\) a 4 nuplets

S2: la jointure

Supports complémentaires:

Toutes les requêtes exprimables avec l’algèbre relationnelle peuvent se construire avec les 6 opérateurs présentés ci-dessus. En principe, on pourrait donc s’en contenter. En pratique, il existe d’autres opérations, très couramment utilisées, qui peuvent se contruire par composition des opérations de base. La plus importante est la jointure.

L’opérateur \(\Join\)

Afin de comprendre l’intérêt de cet opérateur, regardons le produit cartésien \(\rm{Logement} \times \rm{Activité}\), dont le résultat est rappelé ci-dessous.

code

nom

capacité

type

lieu

codeLogement

codeActivité

ca

Causses

45

Auberge

Cévennes

ca

Randonnée

ge

Génépi

134

Hôtel

Alpes

ca

Randonnée

pi

U Pinzutu

10

Gîte

Corse

ca

Randonnée

ta

Tabriz

34

Hôtel

Bretagne

ca

Randonnée

ca

Causses

45

Auberge

Cévennes

ge

Piscine

ge

Génépi

134

Hôtel

Alpes

ge

Piscine

pi

U Pinzutu

10

Gîte

Corse

ge

Piscine

ta

Tabriz

34

Hôtel

Bretagne

ge

Piscine

ca

Causses

45

Auberge

Cévennes

ge

Ski

ge

Génépi

134

Hôtel

Alpes

ge

Ski

pi

U Pinzutu

10

Gîte

Corse

ge

Ski

ta

Tabriz

34

Hôtel

Bretagne

ge

Ski

ca

Causses

45

Auberge

Cévennes

pi

Plongée

ge

Génépi

134

Hôtel

Alpes

pi

Plongée

pi

U Pinzutu

10

Gîte

Corse

pi

Plongée

ta

Tabriz

34

Hôtel

Bretagne

pi

Plongée

ca

Causses

45

Auberge

Cévennes

pi

Voile

ge

Génépi

134

Hôtel

Alpes

pi

Voile

pi

U Pinzutu

10

Gîte

Corse

pi

Voile

ta

Tabriz

34

Hôtel

Bretagne

pi

Voile

Si vous regardez attentivement cette relation, vous noterez que le résultat comprend manifestement un grand nombre de nuplets qui ne nous intéressent pas. C’est le cas de toutes les lignes pour lesquelles le code (provenant de la table Logement) et le codeLogement (provenant de la table Activité) sont distincts. Cela ne présente pas beaucoup de sens (à priori) de rapprocher des informations sur l’hôtel Génépi, dans les Alpes, avec l’activité de plongée en Corse.

Note

Il est bien sûr arbitraire de dire qu’un résultat « n’a pas de sens » ou « ne présente aucun intérêt ». Nous nous plaçons ici dans un contexte où l’on cherche à reconstruire une information sur certaines entités du monde réel, dont la description a été distribuée dans plusieurs tables par la normalisation. C’est l’utilisation sans doute la plus courante de SQL.

Si, en revanche, on considère le produit cartésien comme un résultat intermédiaire, on voit qu’il permet d’associer des nuplets initialement répartis dans des tables distinctes. Sur notre exemple, on rapproche les informations générales sur un logement et la liste des activités de ce logement.

La sélection qui effectue une rapprochement pertinent est celle qui ne conserve que les nuplets partageant la même valeur pour les attributs code et codeLogement, soit:

\[\sigma_{code=codeLogement}(\rm{Logement} \times \rm{Activité})\]

Prenez bien le temps de méditer cette opération de sélection: nous ne voulons conserver que les nuplets de \(\rm{Logement} \times \rm{Activité}\) pour lesquelles l’identifiant du logement (provenant de Logement) est identique à celui provenant de Activité. En regardant le produit cartésien ci-dessous, vous devriez pouvoir vous convaincre que cela revient à conserver les nuplets qui ont un sens: chacune contient des informations sur un logement et sur une activité dans ce même logement.

On obtient le résultat ci-dessous.

code

nom

capacité

type

lieu

codeLogement

codeActivité

ca

Causses

45

Auberge

Cévennes

ca

Randonnée

ge

Génépi

134

Hôtel

Alpes

ge

Piscine

ge

Génépi

134

Hôtel

Alpes

ge

Ski

pi

U Pinzutu

10

Gîte

Corse

pi

Plongée

pi

U Pinzutu

10

Gîte

Corse

pi

Voile

On a donc effectué une composition de deux opérations (un produit cartésien, une sélection) afin de rapprocher des informations réparties dans plusieurs relations, mais ayant des liens entre elles (toutes les informations dans un nuplet du résultat sont relatives à un seul logement). Cette opération est une jointure, que l’on peut directement, et simplement, noter :

\[\rm{Logement} \Join_{code=codeLogement} \rm{Activité}\]

La jointure consiste donc à rapprocher les nuplets de deux relations pour lesquelles les valeurs d’un (ou plusieurs) attributs sont identiques. De fait, dans la plupart des cas, ces attributs communs sont (1) la clé primaire de l’une des relations et (2) la clé étrangère dans l’autre relation. Dans l’exemple ci-dessus, c’est le cas pour code (clé primaire de Logement) et codeLogement (clé étrangère dans Activité).

Note

Le logement Tabriz, qui ne propose pas d’activité, n’apparaît pas dans le résultat de la jointure. C’est normal et conforme à la définition que nous avons donnée, mais peut parfois apparaître comme une contrainte. Nous verrons dans le chapitre final sur SQL que ce dernier propose une variante, la jointure externe, qui permet de la contourner.

La notation de la jointure, \(R \Join_F S\), est un racourci pour \(\sigma_F(R \times S)\).

Note

Le critère de rapprochement, \(F\), peut être n’importe quelle opération de comparaison liant un attribut de \(R\) à un attribut de \(S\). En pratique, on emploie peu les \(\not=\) ou “<” qui sont difficiles à interpréter, et on effectue des égalités.

Si on n’exprime pas de critère de rapprochement, la jointure est équivalente à un produit cartésien.

Initialement, SQL ne proposait pour effectuer la jointure que la version déclarative.

select *
from Logement as l, Activité as a
where l.code=a.codeLogement

En 1992, la révision de la norme a introduit l’opérateur algébrique qui, comme le produit cartésien, et pour les mêmes raisons, prend place dans le from.

select *
from Logement join Activité on (code=codeLogement)

Il s’agit donc d’une manière alternative d’exprimer une jointure. Laquelle est la meilleure? Aucune, puisque toutes les deux ne sont que des spécifications, et n’imposent en aucun cas au système une méthode particulière d’exécution. Il est d’ailleurs exclu pour un système d’appliquer aveuglément la définition de la jointure et d’effectuer un produit cartésien, puis une sélection, car il existe des algorithmes d’évaluation bien plus efficaces.

Résolution des ambiguités

Il faut être attentif aux ambiguités dans le nommage des attributs qui peut survenir dans la jointure au même titre que dans le produit cartésien. Les solutions à employer sont les mêmes : on préfixe par le nom de la relation ou par un synonyme, ou bien on renomme des attributs avant d’effectuer la jointure.

Supposons que l’on veuille obtenir les voyageurs et les séjours qu’ils ont effectués. La jointure s’exprime en principe comme suit:

select *
from Voyageur join Séjour on (idVoyageur=idVoyageur)

Le système renvoie une erreur: La clause de jointure on (idVoyageur=idVoyageur) est clairement ambigüe. Pour MySQL, le message est par exemple Column “idVoyageur” in on clause is ambiguous. Nouvelle tentative:

select *
from Voyageur join Séjour on (Voyageur.idVoyageur=Séjour.idVoyageur)

Nouveau message d’erreur (cette fois, sous MySQL: Encountered duplicate field name: “idVoyageur”). La liste des noms d’attribut dans le nuplet-résultat obtenu avec select * comprend encore deux fois idVoyageur.

Première solution: on renomme les attributs du nuplet résultat. Cela suppose d’énumérer tous les attributs.

select V.idVoyageur as idV1, V.nom, S.idVoyageur as idV2, début, fin
from Voyageur as V join Séjour as S  on (V.idVoyageur=S.idVoyageur)

Cette première solution consiste à effectuer un renommage après la jointure. Une autre solution est d’effectuer le renommage avant la jointure.

select *
from (select idVoyageur as idV1, nom from Voyageur) as V
               join
     (select idVoyageur as idV2, début, fin from Séjour) as S
           on (V.idV1=S.idV2)

En algèbre, la requête ci-dessus correspond à l’expression suivante:

\[(\rho_{idVoyageur \to idV1} (\pi_{idVoyageur, nom}Voyageur) \Join_{idV1=idV2} \rho_{idVoyageur \to idV2} (\pi_{idVoyageur, début, fin}Séjour))\]

On voit que le from commence à contenir des expressions de plus en plus complexes. Dans ses premières versions, SQL ne permettait pas des constructions algébriques dans le from, ce qui avait l’avantage d’éviter des constructions qui ressemblent de plus en plus à de la programmation. Rappelons qu’il existe une syntaxe alternative à la requête ci-dessus, dans la forme déclarative de SQL étudiée au chapitre précédent.

select V.idVoyageur as idV1, V.nom, S.idVoyageur as idV2, début, fin
from Voyageur as V, Séjour as S
where V.idVoyageur= S.idVoyageur

Bref, vous commencez à avoir l’embarras du choix.

La jointure dite « naturelle »

Il reste à vrai dire, avec SQL, un troisième choix, la jointure dite « naturelle ». Elle s’applique uniquement quand les attributs de jointure ont des noms identiques dans les deux tables. C’est le cas ici, (l’attribut de jointure est idVoyageur, que ce soit dans Logement ou dans Séjour). La jointure naturelle s’effectue alors automatiquement sur ces attributs communs, et ne conserve que l’un des attributs dans le résultat, ce qui élimine l’ambiguité. La syntaxe devient alors très simple.

select *
from Voyageur as V natural join Séjour

Si les attributs de jointures sont nommés différemment, la jointure naturelle devient plus délicate à utiliser puisqu’il faut au préalable effectuer des renommages pour faire coïncider les noms des attributs à comparer.

À partir de là, vous savez comment effectuer plusieurs jointures. Un exemple devrait suffire: supposons que l’on veuille les noms des voyageurs et les noms des logements qu’ils ont visités. La requête algébrique devient un peu compliquée. On va s’autoriser une construction en plusieurs étapes.

Tout d’abord on effectue un renommage sur la table Voyageur pour éviter les futures ambiguités.

\[V2 := \rho_{idVoyageur\to idV, nom \to nomVoyageur} (Voyageur)\]

Opération semblable sur les logements.

\[L2 := \rho_{nom \to nomLogement} (Logement)\]

Et finalement, voici la requête algébrique complète, utilisant V2 et L2.

\[\pi_{nomVoyageur, nomLogement} (\rm{L2}) \Join_{code=codeLogement} \rm{Séjour}) \Join_{idVoyageur=idV} V2)\]

En SQL, il faut tout écrire avec une seule requête. Allons-y

select nomVoyageur, nomLogement
from ( (select idVoyageur as idV, nom as nomVoyageur from Voyageur) as V
                 join
            Séjour as S on idV=idVoyageur)
             join
         (select code, nom as nomLogement from Logement) as L
             on codeLogement = code

Ce n’est pas très lisible… Pour comparaison, la version déclarative de ces jointures.

select V.nom as nomVoyageur, L.nom as nomLogement
from   Voyageur as V, Séjour as S, Logement as L
where  V.idVoyageur = S.idVoyageur
and    S.codelogement = L. code

À vous de voir quel style (ou mélange des styles) vous souhaitez adopter.

Quiz

Voici trois requêtes SQL sur la base des films

select titre, nom
from   Film cross join Artiste
where   idRéalisateur = idArtiste

select titre, nom
from   Film  join Artiste on  (idRéalisateur = idArtiste)

select titre, nom
from   Film as f, Artiste as a
where f.idRéalisateur = a.idArtiste

Quelle affirmation est fausse?

  1. La première est incorrecte car elle mélange l’approche déclarative et l’approche algébrique

  2. La seconde est équivalente à la première

  3. Elles sont toutes équivalentes

Voici une requête SQL sur la base des logements

select  idSéjour, codeLogement, codeActivité
from   Séjour join Activité on (codeLogement=codeLogement)

Cette requête est incorrecte syntaxiquement à cause des problèmes d’ambiguités de codeLogement.

Quelle reformulation, parmi les suivantes, est incorrecte?

  1. En préfixant les attributs par le nom des tables dans le from.

    select  idSéjour, codeLogement, codeActivité
from   Séjour join Activité on (Séjour.codeLogement=Activité.codeLogement)

  2. En utilisant des synonymes

    select  idSéjour, S.codeLogement, codeActivité
from   Séjour as S join Activité as A on (S.codeLogement=A.codeLogement)

  3. En utilisant la jointure naturelle

    select  idSéjour, codeLogement, codeActivité
from   Séjour natural join Activité

  4. En renommant avant la jointure

    select  idSéjour, codeLogement, codeActivité
from   (select idSéjour, codeLogement from Séjour) as S
     join
       (select codeActivité, codeLogement as codeL from Activité) as A
     on (codeLogement = codeL)

Je veux utiliser la jointure naturelle pour joindre la table des logements et celle des activités. Les attributs de jointure ont des noms différents, et je dois donc appliquer un renommage. Quelle version est correcte?

  1. En renommant dans la clause select

    select  L.codeLogement as codeL, A.codeLogement as codeL, codeActivité
from   Logement as L natural join Activité as A

  2. En renommant dans la clause from

    select  code, codeActivité
from   (select * from Logement) as L
      natural join
      (select codeLogement as code, codeActivité from Activité) as A

Que calcule la jointure naturelle si les schémas sont totalement distincts (aucun nom d’attribut en commun)?

  1. Une union

  2. Un produit cartésien

  3. Une intersection

Que calcule la jointure naturelle si les schémas sont identiques?

  1. Une union

  2. Un produit cartésien

  3. Une intersection

S3: Expressions algébriques

Supports complémentaires:

Cette section est consacrée à l’expression de requêtes algébriques complexes impliquant plusieurs opérateurs. On utilise la composition des opérations, rendue possible par le fait que tout opérateur produit en sortie une relation sur laquelle on peut appliquer à nouveau des opérateurs.

Note

Les expressions sont seulement données dans la forme concise de l’algèbre. La syntaxe SQL équivalente est à faire à titre d’exercices (et à tester sur notre site).

Sélection généralisée

Regardons d’abord comment on peut généraliser les critères de sélection de l’opérateur \(\sigma\). Jusqu’à présent on a vu comment sélectionner des nuplets satisfaisant un critère de sélection, par exemple : « les logements de type “Hôtel” ». Maintenant supposons que l’on veuille retrouver les hôtels dont la capacité est supérieure à 100. On peut exprimer cette requête par une composition :

\[\sigma_{capacité>100}(\sigma_{type='Hôtel'}(Logement))\]

Ce qui revient à pouvoir exprimer une sélection avec une conjonction de critères. La requête précédente est donc équivalente à celle ci-dessous, où le \(\land\) dénote le “et”.

\[\sigma_{capacité>100 \land type='Hôtel'}(Logement)\]

La composition de plusieurs sélections revient à exprimer une conjonction de critères de recherche. De même la composition de la sélection et de l’union permet d’exprimer la disjonction. Voici la requête qui recherche les logements qui sont en Corse, ou dont la capacité est supérieure à 100.

\[\sigma_{capacité>100}(Logement) \cup \sigma_{lieu='Corse'}(Logement)\]

Ce qui permet de s’autoriser la syntaxe suivante, où le “\(\lor\)” dénote le “ou”.

\[\sigma_{capacité>100\ \lor\ lieu='Corse'}(Logement)\]

Enfin la différence permet d’exprimer la négation et « d’éliminer » des nuplets. Par exemple, voici la requête qui sélectionne les logements dont la capacité est supérieure à 200 mais qui ne sont pas aux Antilles.

\[\sigma_{capacité>100}(Logement) - \sigma_{lieu='Corse'}(Logement)\]

Cette requête est équivalente à une sélection où on s’autorise l’opérateur “\(\not=\)” :

\[\sigma_{capacité>100 \land lieu \not='Corse'}(Logement)\]

Important

Attention avec les requêtes comprenant une négation, dont l’interprétation est parfois subtile. D’une manière générale, l’utilisation du “\(\not=\)” n’est pas équivalente à l’utilisation de la différence, l’exemple précédent étant une exception. Voir la prochaine section.

En résumé, les opérateurs d’union et de différence permettent de définir une sélection \(\sigma_F\) où le critère \(F\) est une expression booléenne quelconque. Attention cependant : si toute sélection avec un “ou” peut s’exprimer par une union, l’inverse n’est pas vrai (exercice).

Requêtes conjonctives

Les requêtes dites conjonctives constituent l’essentiel des requêtes courantes. Intuitivement, il s’agit de toutes les recherches qui s’expriment avec des “et”, par opposition à celles qui impliquent des “ou” ou des “not”. Dans l’algèbre, ces requêtes sont toutes celles qui peuvent s’écrire avec seulement trois opérateurs : \(\pi\), \(\sigma\), \(\times\) (et donc, indirectement, \(\Join\)).

Les plus simples sont celles où on n’utilise que \(\pi\) et \(\sigma\). En voici quelques exemples.

  • Nom des logements en Corse :

    \(\pi_{nom}(\sigma_{lieu='Corse'}(Logement))\)

  • Code des logements où l’on pratique la voile.

    \(\pi_{codeLogement}(\sigma_{codeActivité='Voile'}(Activité))\)

  • Nom et prénom des clients corses

    \(\pi_{nom,prénom}(\sigma_{région='Corse'}(Voyageur))\)

Des requêtes légèrement plus complexes - et extrêmement utiles - sont celles qui impliquent la jointure. On doit utiliser la jointure dès que les attributs nécessaires pour évaluer une requête sont réparties dans au moins deux relations. Ces « attributs nécessaires » peuvent être :

  • Soit des attributs qui figurent dans le résultat ;

  • Soit des attributs sur lesquels on exprime un critère de sélection.

Considérons par exemple la requête suivante : « Donner le nom et le lieu des logements où l’on pratique la voile ». Une analyse très simple suffit pour constater que l’on a besoin des attributs lieu et nom qui apparaîssent dans la relation Logement, et de codeActivité qui apparaît dans Activité.

Donc il faut faire une jointure, de manière à rapprocher les nuplets de Logement et de Activité. Il reste donc à déterminer le (ou les) attribut(s) sur lesquels se fait ce rapprochement. Ici, comme dans la plupart des cas, la jointure permet de « recalculer » l’association entre les relations Logement et Activité. Elle s’effectue donc par appariement de la clé primaire d’une part (dans Logement), de la clé étrangère d’autre part.

\[\pi_{nom,lieu}(Logement \Join_{code=codeLogement} (\sigma_{codeActivité='Voile'}(\text{Activité})) )\]

En pratique, la grande majorité des opérations de jointure s’effectue sur des attributs qui sont clé primaire dans une relation, et clé étrangère dans l’autre. Il ne s’agit pas d’une règle absolue, mais elle résulte du fait que la jointure permet le plus souvent de reconstituer le lien entre des informations qui sont naturellement associées (comme un logement et ses activités, ou un logement et ses clients), mais qui ont été réparties dans plusieurs relations au moment de la conception de la base. Voir le chapitre Conception d’une base de données à ce sujet.

Voici quelques autres exemples qui illustrent cet état de fait :

  • Nom des clients qui sont allés à Tabriz (en supposant connu le code, ta, de cet hôtel) :

    \[\pi_{nom} (\text{Voyageur} \Join_{idVoyageur=idVoyageur} \sigma_{codeLogement='ta'} (\text{Séjour}))\]

  • Quels lieux a visité le client 30 :

    \[\pi_{lieu} (\sigma_{idVoyageur=30} (\text{Séjour}) \Join_{codeLogement=code} (\text{Logement}))\]

  • Nom des clients qui ont eu l’occasion de faire de la voile :

    \[\pi_{nom} (\texttt{Voyageur} \Join_{idVoyageur=idVoyageur} (\texttt{Séjour} \Join_{codeLogement=codeLogement} \sigma_{codeActivité='Voile'}(\texttt{Activité})))\]

    Note

    Pour simplifier un peu l’expression, on a considéré ci-dessus que l’ambiguité sur l’attribut de jointure idVoyageur était effacée par la projection finale sur nom. En toute rigueur, la relation obtenue par

    \[\texttt{Voyageur} \Join_{idVoyageur=idVoyageur} (\texttt{Séjour} \Join_{codeLogement=codeLogement} \sigma_{codeActivité='Voile'}(\texttt{Activité}))\]

    comporte des noms d’attributs doublés auxquels il faudrait appliquer un renommage.

La dernière requête comprend deux jointures, portant à chaque fois sur des clés primaires et/ou étrangères. Encore une fois ce sont les clés qui définissent les liens entre les relations, et elle servent donc naturellement de support à l’expression des requêtes.

Voici maintenant un exemple qui montre que cette règle n’est pas systématique. On veut exprimer la requête qui recherche les noms des clients qui sont partis en vacances dans leur lieu de résidence, ainsi que le nom de ce lieu.

Ici on a besoin des informations réparties dans les relations Logement, Séjour et Voyageur. Voici l’expression algébrique :

\[\pi_{nom, lieu} (\text{Voyageur} \Join_{idVoyageur=idVoyageur \land région=lieu} (\text{Séjour} \Join_{codeLogement=code} \text{Logement}))\]

Les jointures avec la relation Séjour se font sur les couples (clé primaire, clé étrangère), mais on a en plus un critère de rapprochement relatif à l’attribut lieu de Voyageur et de Logement.

Requêtes avec \(\cup\) et \(-\)

Pour finir, voici quelques exemples de requêtes impliquant les deux opérateurs \(\cup\) et \(-\). Leur utilisation est moins fréquente, mais elle peut s’avérer absolument nécessaire puisque ni l’un ni l’autre ne peuvent s’exprimer à l’aide des trois opérateurs « conjonctifs » étudiés précédemment. En particulier, la différence permet d’exprimer toutes les requêtes où figure une négation : on veut sélectionner des données qui ne satisfont pas telle propriété, ou tous les « untels » sauf les “x” et les “y”, etc.

Illustration concrète sur la base de données avec la requête suivante : quels sont les codes des logements qui ne proposent pas de voile ?

\[\pi_{code}(\text{Logement}) - \pi_{codeLogement}(\sigma_{codeActivité='Voile'}(\text{Activité}))\]

Comme le suggère cet exemple, la démarche générale pour construire une requête du type « Tous les \(O\) qui ne satisfont pas la propriété \(p\) » est la suivante :

  • Construire une première requête \(A\) qui sélectionne tous les \(O\).

  • Construire une deuxième requête \(B\) qui sélectionne tous les \(O\) qui satisfont \(p\).

  • Finalement, faire \(A - B\).

Les requêtes \(A\) et \(B\) peuvent bien entendu être arbitrairement complexes et mettre en œuvre des jointures, des sélections, etc. La seule contrainte est que le résultat de \(A\) et de \(B\) comprenne le même nombre d’attributs (et, en théorie, les mêmes noms, mais on peut s’affranchir de cette contrainte).

Important

Attention à ne pas considérer que l’utilisation du comparateur \(\not=\) est équivalent à la différence. La requête suivante par exemple ne donne pas les logements qui ne proposent pas de voile

\[\pi_{codeLogement}(\sigma_{codeActivité\ \not=\ 'Voile'}(\text{Activité}))\]

Pas convaincu(e)? Réfléchissez un peu plus, faites le calcul concret. C’est l’un de pièges à éviter.

Voici quelques exemples complémentaires qui illustrent ce principe.

  • Régions où il y a des clients, mais pas de logement.

    \[\pi_{région} (\text{Voyageur}) - \pi_{région}(\rho_{lieu \to région} (\text{Logement}))\]

  • Identifiant des logements qui n’ont pas reçu de client tibétain.

    \[\pi_{code}(\text{Logement}) - \pi_{codeLogement} (\text{Séjour} \Join_{idVoyageur=idVoyageur} \sigma_{région='Tibet'} (\text{Voyageur}))\]

  • Id des clients qui ne sont pas allés en Corse.

    \[\pi_{idVoyageur}(\text{Voyageur}) - \pi_{idVoyageur}(\sigma_{lieu='Corse'}(\text{Logement}) \Join_{code=codeLogement} \text{Séjour})\]

La dernière requête construit l’ensemble des idVoyageur pour les clients qui ne sont pas allés en Corse. Pour obtenir le nom de ces clients, il suffit d’ajouter une jointure (exercice).

Complément d’un ensemble

La différence peut être employée pour calculer le complément d’un ensemble. Prenons l’exemple suivant : on veut les ids des clients et les logements où ils ne sont pas allés. En d’autres termes, parmi toutes les associations Voyageur/Logement possibles, on veut justement celles qui ne sont pas représentées dans la base !

C’est un des rares cas où le produit cartésien seul est utile : il permet justement de constituer « toutes les associations possibles ». Il reste ensuite à en soustraire celles qui sont dans la base avec l’opérateur \(-\).

\[(\pi_{idVoyageur}(\text{Voyageur}) \times \pi_{code}(\text{Logement})) - \pi_{idVoyageur, codeLogement} (\text{Séjour})\]

Quantification universelle

Enfin la différence est nécessaire pour les requêtes qui font appel à la quantification universelle : celles où l’on demande par exemple qu’une propriété soit toujours vraie. À priori, on ne voit pas pourquoi la différence peut être utile dans de tels cas. Cela résulte simplement de l’équivalence suivante : une propriété est vraie pour tous les éléments d’un ensemble si et seulement si il n’existe pas un élément de cet ensemble pour lequel la propriété est fausse. La quantification universelle s’exprime par une double négation.

En pratique, on se ramène toujours à la seconde forme pour exprimer des requêtes. Prenons un exemple : quels sont les clients dont tous les séjours ont eu lieu en Corse? On l’exprime également par “quels sont clients pour lesquels il n’existe pas de séjour dans un lieu qui soit différent de la Corse. Ce qui donne l’expression suivante :

\[\pi_{idVoyageur} (\text{Séjour}) - \pi_{idVoyageur}(\sigma_{lieu \not='Corse'}(\text{Séjour}))\]

Pour finir, voici une des requêtes les plus complexes, la division. L’énoncé (en français) est simple, mais l’expression algébrique ne l’est pas du tout. L’exemple est le suivant : on veut les ids des clients qui sont allés dans tous les logements.

Traduit avec (double) négation, cela donne : les ids des clients tels qu’il n’existe pas de logement où ils ne soient pas allés. Ce qui donne l’expression algébrique suivante :

\[\pi_{idVoyageur}(\text{Voyageur}) - \pi_{idVoyageur} ((\pi_{idVoyageur}(\text{Voyageur}) \times \pi_{code}(\text{Logement})) - \pi_{idVoyageur, idLogement} (\text{Séjour}))\]

Explication: on réutilise l’expression donnant les clients et les logements où ils ne sont pas allés (voir plus haut) :

\[\pi_{idVoyageur}(\text{Voyageur}) \times \pi_{code}(\text{Logement})) - \pi_{idVoyageur, idLogement} (\text{Séjour})\]

On obtient un ensemble \(B\). Il reste à prendre tous les clients, sauf ceux qui sont dans \(B\).

\[\pi_{idVoyageur}(\text{Voyageur}) - B\]

Ce type de requête est rare (heureusement) mais illustre la capacité de l’algèbre à exprimer par de simples manipulations ensemblistes des opérations complexes.

Quiz

Supposons que nous ayons une requête \(\pi_U(\sigma_C(E))\). Est-ce que nous pouvons la réécrire en \(\sigma_C(\pi_U(E))\) pour obtenir une requête équivalente (qui calcule toujours le même résultat) ?

  1. Oui, toujours

  2. Oui si la condition C est de la forme attribut = valeur et non si c’est attribut = attribut

  3. Non parce que \(\sigma_C(\pi_U(E))\) les conditions dans \(C\) peuvent porter sur des attributs qui ne sont pas dans \(U\)

  4. Non parce qu’il est possible que les deux requêtes donnent des résultats différents

Parmi les expressions algébriques suivantes, laquelle peut se réécrire avec une simple sélection dans laquelle on autorise le “ou” logique?

  1. \(\sigma_{X=3}(R) \cup \sigma_{Y=2} (R)\)

  2. \(\sigma_{X=3}(R) \cup \sigma_{Y=2} (S)\)

  3. \(\sigma_{X=3}(R) \cup \sigma_{X=3} (S)\)

Voici une expression algébrique \(\sigma_F(R)\) avec une sélection complexe

\[F = ( A=1 \lor B = 2 ) \land not (A=D ).\]

Quelle réécriture avec des sélections élémentaires est-elle correcte?

  1. \((\sigma_{A=1} (\sigma_{B=2} (R) )) - \sigma_{A=D} (R)\)

  2. \((\sigma_{A=1} (R) - \sigma_{A=D} (R) ) \cup \sigma_{B=2} (R) )\)

  3. \((\sigma_{A=1} (R) \cup \sigma_{B=2} (R) ) - \sigma_{A=D} (R)\)

Voici une table \(R\).

A

B

C

D

1

0

1

2

4

1

2

2

6

0

6

3

7

1

1

3

1

0

1

1

1

1

1

1

Et la condition :

\[F = ( A=1 \lor A=B ) \land ( not ( B=2 \land C=D ) \land A=D ).\]

Combien de nuplets \(\sigma_F(R)\) contient-il ?

  1. 0

  2. 1

  3. 2

  4. 3

  5. 4

  6. 5

Vous demandez la liste des voyageurs qui ne sont pas allés en Corse. On vous propose la requête suivante:

\[\pi_{idVoyageur}(\sigma_{lieu \not= 'Corse'}(\text{Logement}) \Join_{code=codeLogement} \text{Séjour})\]

Est-elle correcte?

  1. Oui, car un voyageur sélectionné par cette requête n’est pas allé en Corse, et répond donc au critère voulu.

  2. Non, car un voyageur sélectionné par cette requête est allé ailleurs qu’en Corse, ce qui ne prouve pas qu’il n’y est pas allé pour un autre séjour

S4: Complément: évaluation et optimisation

Ce complément introduit la manière dont un SGBD analyse, optimise et exécute une requête. Il est présenté dans le but de vous donner un aperçu de l’utilité de l’algèbre dans un contexte d’exécution de requêtes, mais ne fait pas partie du contenu du cours soumis à examen.

Supports complémentaires:

SQL étant un langage déclaratif dans lequel on n’indique ni les algorithmes à appliquer, ni les chemins d’accès aux données, le système a toute latitude pour déterminer ces derniers et les combiner de manière à obtenir les meilleures performances.

Nous avons une requête, exprimée en SQL, soumise au système. Comme vous le savez, SQL permet de déclarer un besoin, mais ne dit pas comment calculer le résultat. C’est au système de produire une forme operatoire, un programme, pour effectuer ce calcul. Notez que cette approche a un double avantage. Pour l’utilisateur, elle permet de ne pas se soucier d’algorithmique d’exécution. Pour le système elle laisse la liberté du choix de la meilleure méthode. C’est ce qui fonde l’optimisation, la liberté de déterminer la manière de répondre a un besoin.

_images/exec-optim-1.png

Fig. 19 Les requêtes SQL sont déclaratives

En base de données, le programme qui évalue une requête a une forme très particulière. On l’appelle plan d’exécution. Il a la forme d’un arbre constitue d’opérateurs qui échangent des données. Chaque opérateur effectue une tache précise et restreinte: transformation, filtrage, combinaisons diverses. Comme nous le verrons, un petit nombre d’opérateurs suffit a évaluer des requêtes, même très complexes. Cela permet au système de construire très rapidement, a la volée, un plan et de commencer a l’exécuter. La question suivante est d’étudier comment le système passe de la requête au plan.

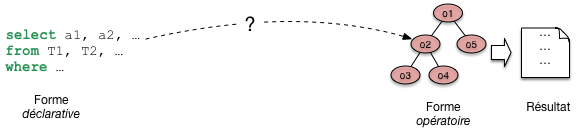
_images/exec-optim-2.png

Fig. 20 De la requête SQL au plan d’exécution.

Le passage de SQL a un plan s’effectue en deux étapes, que j’appellerai a et b. Dans l’étape a on tire partie de l’équivalence entre SQL, ou une grande partie de SQL, avec l’algèbre. Pour toute requêtes on peut donc produire une expression de l’algèbre. Et ici on trouve déjà une forme opérationnelle, qui nous dit quelles opérations effectuer. Nous l’appellerons plan d’execution logique. Une expression de l’algèbre peut se représenter comme un arbre, et nous sommes déjà proche d’un n plan d’exécution. Il reste assez abstrait.

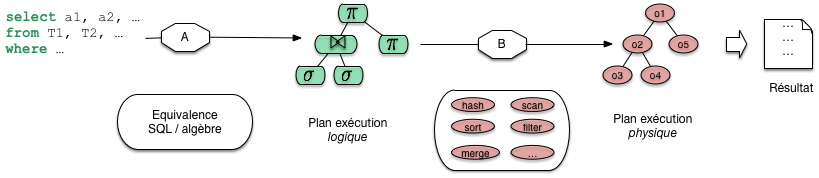
_images/exec-optim-3.png

Fig. 21 Les deux phases de l’optimisation

Ce n’est pas tout a fait suffisant. Dans l’étape b le système va choisir des opérateurs particulière, en fonction d’un contexte spécifique. Ce peut être là présence ou non d’index, la taille des tables, la mémoire disponible. Cette étape b donne un plan d’exécution physique, applicable au contexte.

Reste la question de l’optimisation. Il faut ici élargir le schéma: a étape, a ou b, plusieurs options sont possibles. Pour l’étape a, c’est la possibilité d’obtenir plusieurs expressions équivalentes. La figure montre par exemple deux combinaisons possibles issues de la même requête sql. Pour l’étape les options sont liées au choix de l’algorithmique, des opérateurs as exécuter.

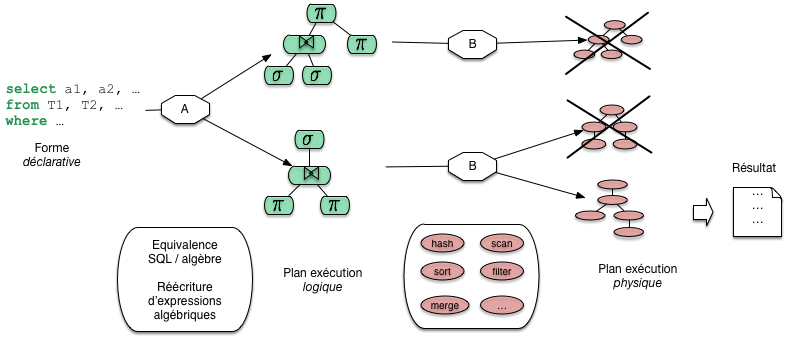
_images/exec-optim-4.png

Fig. 22 Processus général d’optimisation et d’évaluation

Cette figure nous donne la perspective générale de cette partie du cours. Nous allons étudier les opérateurs, les plans d’exécution, les transformations depuis une requête SQL, et quelques critères de choix pour l’optimisation.

Exercices

Pour varier les exemples, nous utilisons la base (fictive et simplifiée bien entendu) d’un syndic de gestion d’immeuble. Voici son schéma

  • Immeuble (id, nom, adresse)

  • Appart (id , no , surface , niveau , idImmeuble)

  • Personne (id, prénom , nom , profession , idAppart)

  • Propriétaire (idPersonne , idAppart, quotePart)

Ce schéma et cette base sont fournis respectivement dans les scripts SchemaImmeuble.sql et BaseImmeuble.sql. Vous pouvez les installer localement si vous le souhaitez. La base est également disponible via notre interface en ligne si vous souhaitez effectuer réellement les requêtes proposées parallèlement à votre lecture.

La table Immeuble

Voici le contenu de la table Immeuble.

id

nom

adresse

1

Koudalou

3 rue des Martyrs

2

Barabas

2 allée du Grand Turc

La table Appart

Voici le contenu de la table Appart.

id

no

surface

niveau

idImmeuble

100

1

150

14

1

101

34

50

15

1

102

51

200

2

1

103

52

50

5

1

104

43

75

3

1

200

1

150

0

2

201

2

250

1

2

202

3

250

2

2

La table Personne

Voici le contenu de la table Personne.

id

prénom

nom

profession

idAppart

1

Prof

Enseignant

202

2

Alice

Grincheux

Cadre

103

3

Léonie

Atchoum

Stagiaire

100

4

Barnabé

Simplet

Acteur

102

5

Alphonsine

Joyeux

Rentier

201

6

Brandon

Timide

Rentier

104

7

Don-Jean

Dormeur

Musicien

200

La table Propriétaire

Voici le contenu de la table Propriétaire.

idPersonne

idAppart

quotePart

1

100

33

5

100

67

1

101

100

5

102

100

1

202

100

5

201

100

2

103

100

Exercice Ex-alg-1: gestion des doublons

Dans le modèle théorique, une relation est un ensemble, et ne contient donc aucun doublon. Dans la norme SQL, les choses sont différentes : pour des raisons pratiques, les doublons sont acceptés (les relations sont donc des multiensembles, ou bag en anglais) et on doit toujours se demander en exprimant une requête SQL s’il faut les éliminer avec distinct.

Posons-nous la question pour le produit cartésien. Soit deux relations R(idR, A, B, C, ...) et S(idS, U, V, W, ..) avec pour clés primaires idR et idS. On veut montrer que le distinct est-il toujours inutile dans la requête:

select *
from R cross join S

On montre que le distinct est inutile:

  • Montrer l’unicité de la paire constituée des identifiants dans \(R \times S\).

  • En déduire la propriété cherchée

Exercice Ex-alg-2: du SQL déclaratif à l’expression algébrique

Un SGBD relationnel reçoit une requête SQL, en principe sous forme déclarative, et la traduit alors en expression algébrique, qui donne les opérations à effectuer. À vous de faire le travail: donnez les expressions algébriques équivalentes aux requêtes SQL ci-dessous.

Vous n’avez pas droit aux conjonctions ou disjonctions dans la formule de sélection. Utilisez la composition et l’union.

 select t.code, t.nom, t.type
 from Logement as t
 where t.lieu = 'Corse'

 select t.code, t.nom
 from Logement as t
 where t.type = 'Hôtel' and (t.lieu = 'Alpes' or t.capacité >= 100)

select l.code, l.nom
from Logement as l, Activité as a
where l.code = a.codeLogement
and   a.codeActivité = 'Ski'

select distinct l1.nom as nom1, l2.nom as nom2
from Logement as l1, Logement as l2
where l1.type = l2.type

select distinct v.prénom, v.nom
from Voyageur as v
where exists (select ''
       from Séjour as s, Logement as l
       where v. idVoyageur=s.idVoyageur
       and   s.codeLogement = l .code
       and   l.lieu = 'Alpes')

select distinct l.nom
from Logement as l
where not exists (select ''
          from Activité as a
          where l.code = a.codeLogement
          and a.codeActivité = 'Ski')

Exercice Ex-alg-3: de l’algèbre à SQL algébrique

L’atelier consiste à étudier un ensemble de requêtes algébriques, à exprimer leur signification en bon français, et à donner leur formulation en SQL, forme algébrique.

Note

Le except n’existant pas dans MySQL, vous pouvez exprimer la différence en SQL avec no exists comme nous l’avons vu dans le chapitre précédent.

Vous pouvez alors effectuer cette requête en ligne et vérifier le résultat.

Note

Pour simplifier un peu les expressions, on considère ci-dessous que dans la syntaxe \(R \Join_{A=B} S\), A est toujours un attribut de R et B un attribut de S. Une requête comme \(R \Join_{id=id} S\) ne présente donc pas d’ambiguité.

Voici donc la liste des expressions algébriques à exprimer en SQL (forme algébrique).

  • \(\pi_{nom,profession}(Personne)\)

  • \(\pi_{idImmeuble,id}(\sigma_{surface > 150}(Appart))\)

  • \(\sigma_{no = niveau}(Appart)\)

  • \(\pi_{nom,no,surface}(Immeuble \Join_{id=idImmeuble} Appart)\)

  • \(\pi_{nom,no,surface}(Appart \Join_{id=idAppart} Personne)\)

  • \(\pi_{nom, idAppart}(Propriétaire \Join_{idPersonne=id \land idAppart=idAppart} Personne))\)

  • \(\pi_{nom, nomI,no,surface}(\rho_{id\to idI, nom \to nomI} (Immeuble) \Join_{idI=idImmeuble} (Appart \Join_{id=idAppart} Personne))\)

  • \(\rho_{id \to idAppart} (\pi_{id} (Appart)) - \pi_{idAppart}(Personne)\)

Exercice Ex-alg-4: expressions algébriques

Exprimez les requêtes suivantes, en algèbre relationnelle. Vous avez le droit de décomposer une expression complexe en plusieurs étapes, en donnant un nom à chaque étape.

Par exemple: je cherche le nom de l’occupant de l’appartement numéro 51 dans le Koudalou.

Je dois interroger la table Personne (occupant), Appart (numéro 51) et Immeuble (le Koudalou). Voici une décomposition détaillée.

Tout d’abord je sélectionne le Koudalou, dans une relation temporaire K.

\[K := \rho_{id \to idI} (\pi_{id} (\sigma_{nom=Koudalou} (Immeuble) ))\]

Je prends ensuite l’appartement 51 par jointure entre Appart et K. J’en profite pour ne conserver, par projection, que les attributs qui m’intéressent, avec parfois un renommage, afin d’éviter de futures ambiguités.

\[A51 := \pi_{id51,surface}(\rho_{id \to id51} (\sigma_{no=51} (Appart) \Join_{idImmeuble=idI} K))\]

Il reste à joindre A51 avec la table Personne.

\[\pi_{nom, surface} (Personne \Join_{idAppart=id51} A51)\]

En assemblant le tout on aurait l’expression complète. Si vous essayez d’exprimer cela en SQL, avec les opérateurs ensemblistes, vous devriez être convaincus que la forme déclarative est beaucoup plus claire et économique.

Requêtes

  • Qui habite le Koudalou? Vous pouvez décomposer en

    • Les appartements du Koudalou (identifiant)

    • Occupants de ces appartements

  • Profession des occupants d’un appartement de plus de 100 m2

  • Nom des immeubles ayant un appartement de plus de 150 m2.

  • Qui sont les propriétaires de l’appartement de Atchoum?

  • Dans quels immeubles habite un acteur?

  • Qui habite un appartement de moins de 70 m2

  • Qui est, au moins partiellement, propriétaire de l’appartement qu’il occupe?

  • Qui occupe un appartement possédé par Prof

  • Qui n’est pas propriétaire?

  • Paires de personnes habitant, dans le même immeuble, un appartement de même superficie.

  • Dans quels immeubles ne trouve-t-on aucun musicien?

  • Qui possède un appartement sans l’occuper?

Si vous avez des soucis pour utiliser les lettres grecques, il est possible de les noter en toutes lettres: PI, RHO, SIGMA, CROSS, JOIN, UNION, MINUS.

Exercice Ex-alg-5: réécriture d’expressions algébriques équivalentes

On dispose de deux tables \(T_1(A,B,C)\) et \(T_2(D,E,F)\). Donnez une expression algébrique équivalente à la suivante, dans laquelle on utilise la jointure mais pas le produit cartésien, et où les sélections s’appliquent directement aux tables.

\[\sigma_{A=C \land C > D \land E =F} (T_1 \times T_2)\]